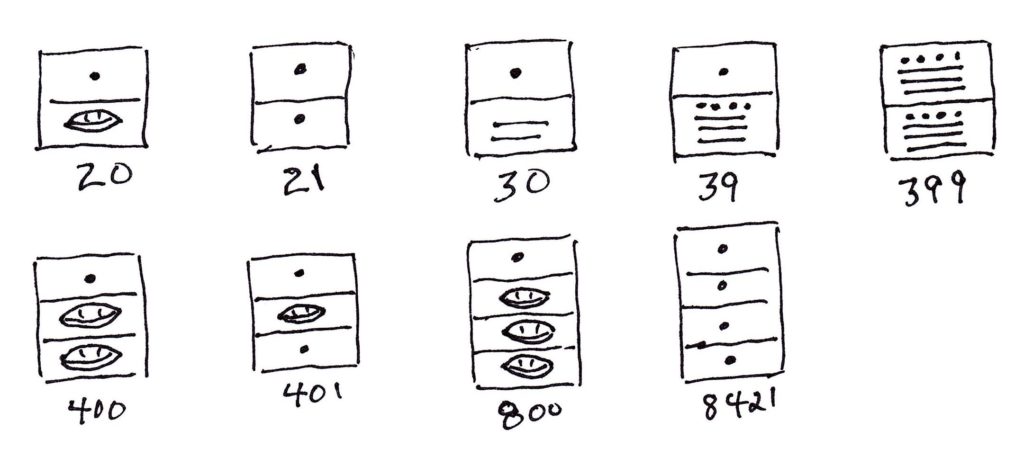
The ancient Maya developed a positional number system based on groups of 20 (“base 20”).
Positional number system? Base 20?
Let’s look at our modern number system to understand those terms:
- Our system is sometimes considered Arabic (even though Arabia obtained this system from India). I will indicate if a number is Arabic (or base 10) for clarity.
- Our system consists of ten symbols: 1, 2, 3, 4, 5, 6, 7, 8, 9, and the null value “0”
- Our system is positional. Each number has a different value depending on its relative position.
- Our system is base 10. Each positional number is a multiple of some power of ten.
For example, take the number 126. Each digit means a different value depending on position. Starting from the right-most digit:
- Six times one (Note: ten to the zero power is “one”).
- Two times ten (or ten to the first power)
- One times ten squared (or ten to the second power).
The Maya number system is base 20. It is positional. But it only uses dots, lines, and a special null symbol which are combined to make twenty symbols:
Larger numbers require extra positions which the Maya stacked vertically (in the following figure, the square are added to help differentiate a lower value from the upper for clarity – the Maya did not use these squares!):
Revisiting our number “126”: To convert 126 (Arabic) into base 20, we first need to determine how the Arabic number 126 can be divided up into groups of twenty:
- twenty times twenty = 400: but there are no groups of 400 in 126 (Arabic)
- twenty: there are six groups of twenty in 126 (Arabic)
- ones: there are six groups of ones in 126 (Arabic)
So 126 in our Arabic system is equivalent to six groups of twenty and six ones. And we know that six is represented by the Maya with a bar and a dot. So we need to use a bar and a dot twice.
In our modern (Arabic) system, the positions are written horizontally, with the ones on the right and the groups of 10 to the left.
But we know that, in the Maya system, the positions are written vertically, with the ones at the bottom and the groups of 20 above the ones.
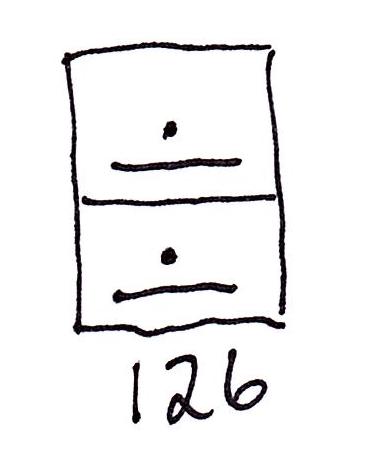
So the value of 126 (Arabic) is written in Maya as
…where the squares are again added for separate the two symbols. The upper symbol gives the number of groups of twenty (6 x 20 = 120). The lower gives the number of ones (6 x 1 = 6). Hence, the two symbols (in the given orientation) describe our Arabic value of 126.
For additional study (and how to add, subtract, multiply, and divide), check out: http://localhs.com/pdf/english_mayan_math.pdf